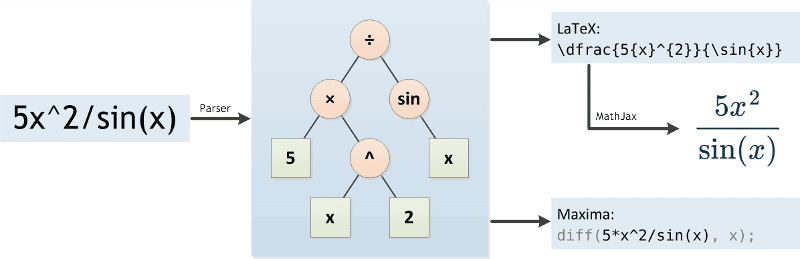
The command diff (f) differentiates f with respect to x ans = 5*cos (5*x) As another example, let g = exp (x)*cos (x);Question Find the derivative with respect to x of the integral from 2 to x^3 of ln(x^2)dx Related Answer More Related Question & AnswersMore Related Question & AnswersWhere f(x) is a function of the variable x, and ' denotes the derivative with respect to the variable x The derivative rule above is given in terms of a function of xHowever, the rule works for single variable functions of y, z, or any other variableJust replace all instances of x in the derivative rule with the applicable variable

How To Do Implicit Differentiation 7 Steps With Pictures
Partial derivative of ln(x^2+y^2) with respect to x
Partial derivative of ln(x^2+y^2) with respect to x-Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and morePlease Subscribe here, thank you!!!




Calculating The Derivative Of Ln X 2 Video Lesson Transcript Study Com
Differentiation To illustrate how to take derivatives using Symbolic Math Toolbox™ software, first create a symbolic expression syms x f = sin (5*x);Mathematics, 1030 alexis3744 Find the derivative of y with respect to x y= ((lnx)/(2lnx))2x d (y 2)×dy = 3 dy dx 2x 2y dy = 3 dx dy = 3 2x dx 2y Example Differentiate a x with respect to x You might be tempted to write xa x1 as the answer This is wrong That would be the answer if we were differentiating with respect to a not x Put y = a x
Definition of Partial Derivatives Let f(x,y) be a function with two variables If we keep y constant and differentiate f (assuming f is differentiable) with respect to the variable x, using the rules and formulas of differentiation, we obtain what is called the partial derivative of f with respect to x which is denoted by Similarly If we keep x constant and differentiate f (assuming f is The derivative of ln(x) with respect to x is (1/x) The derivative of ln(s) with respect to s is (1/s) In a similar way, the derivative of ln(2x) with respect to 2x is (1/2x) We will use this fact as part of the chain rule to find the derivative of ln(2x) with respect to x How to find the derivative of ln(2x) using the Chain RuleIf y = x n1, ln x, then the n th order derivative of y with respect to x at \(x=\dfrac{1}{2}\) is Please scroll down to see the correct answer and solution guide
Video Transcript {'transcript' "this wasn't even a function Why?01 Recall ordinary derivatives If y is a function of x then dy dx is the derivative meaning the gradient (slope of the graph) or the rate of change with respect to x 02 Functions of 2Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




Derivative Calculator Wolfram Alpha
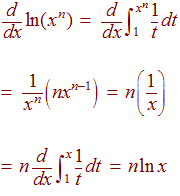



Logs And Derivatives
You can find this function by taking the composition of two functions and then apply the function x 2 to go from x to x 2 You can use the chain rule to find the derivative of this big function with respect to lnx (Kahn has videos on the chain rule) let f ( x) = e x and g ( x) = x 2 then g ( f ( l n ( x)) = x 2 and using the chain rule theDerivative of ln(x), with definition & implicit differentiation, proof of derivative of ln(x), derivative of ln(x) with definition of derivative, derivativeY = ln x then e y = x Now implicitly take the derivative of both sides with respect to x remembering to multiply by dy/dx on the left hand side since it is given in terms of y not x e y dy/dx = 1 From the inverse definition, we can substitute x in for e y to get
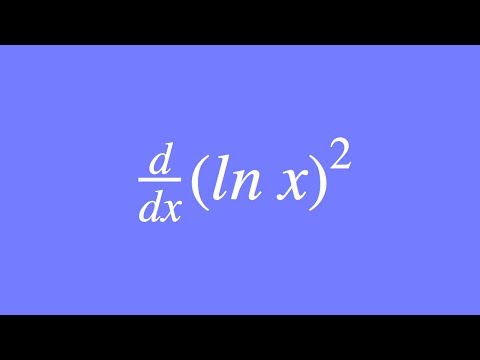



How To Differentiate Ln X 2 Using The Chain Rule Youtube




Consider The Function F X Y Ln X 2 Y 2 3 Compute The Partial Derivatives Of The First And Second Order Mathematics Stack Exchange
What Is a Derivative of Xlnx?(1) If y = x 2, dy/dx = 2x This means that if y = x 2, the derivative of y, with respect to x is 2x (2) d (x 2) = 2x dx This says that the derivative of x 2 with respect to x is 2x (3) If f(x) = x 2, f'(x) = 2x This says that is f(x) = x 2, the derivative of f(x) is 2x Finding the Gradient of a Curve A formula for the gradient of a curve I have a function g as a function of x;
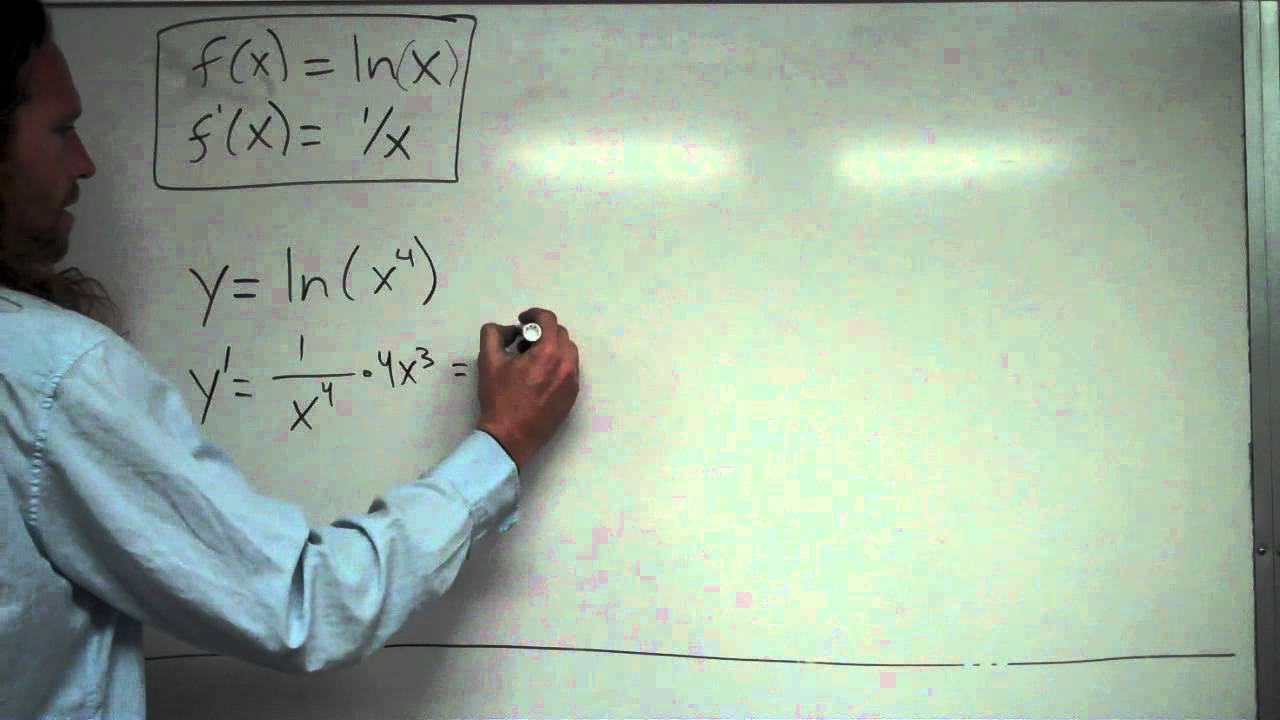



Derivative Of Ln X Youtube




0 Fwd Derivative Ck Y Ln X Lux 2 C Find Denivative Of Sw2x 3 Homeworklib
Let's first think about a function of one variable (x) f(x) = x 2 We can find its derivative using the Power Rule f'(x) = 2x But what about a function of two variables (x and y) f(x, y) = x 2 y 3 We can find its partial derivative with respect to x when we treat y as a constant (imagine y is a number like 7 or something) f' x = 2x 0 = 2xFree implicit derivative calculator implicit differentiation solver stepbystep This website uses cookies to ensure you get the best experience By using thisExplanation we want to calculate dy/dt for x= 9 and we know xy relation so we get y = 3,3 for which we have to calculate dy/dt since y = x^5 , so x= y^2 given is, dx/dt = 12 we substitute x with y^2 so above equation becomes d (y^2)/dt = 12 so, applying chain rule and simplifying we get, dy/dt = 6/y
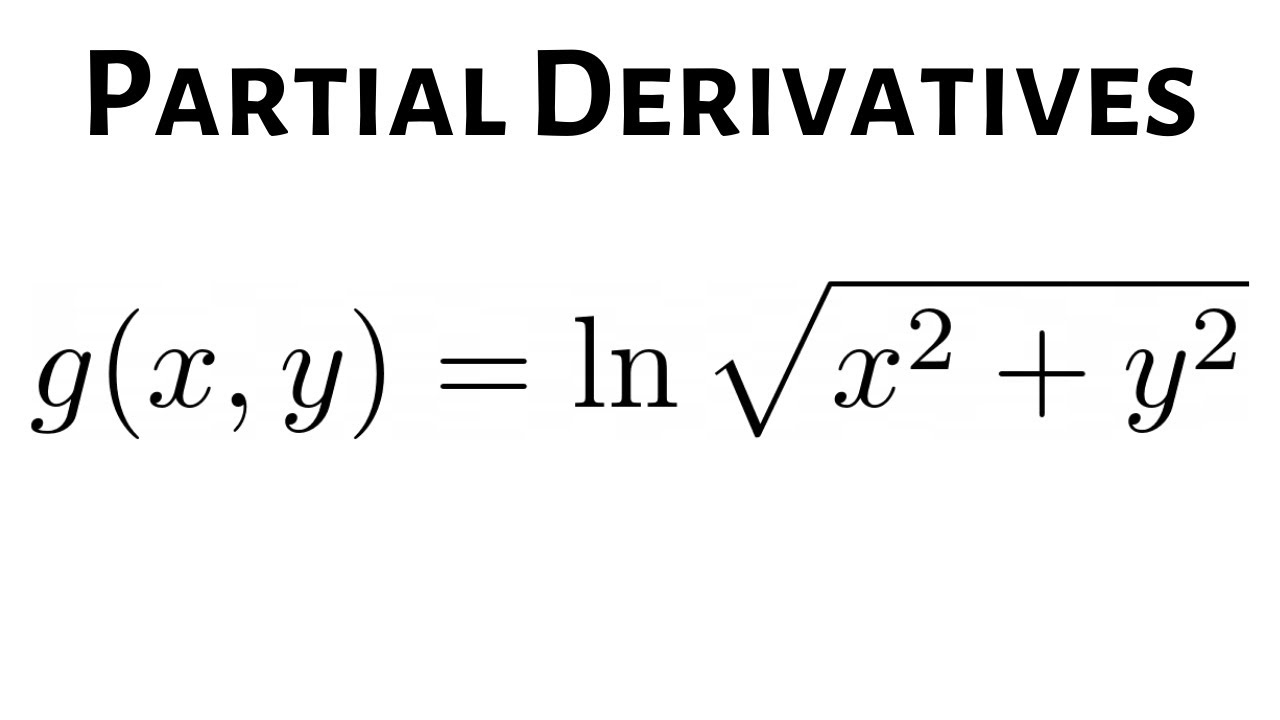



Larson Calculus 13 3 28 First Partial Derivatives Of G X Y Ln Sqrt X 2 Y 2 Youtube



3
Derivative Of Ln(x) Steps to Solve We want to find the derivative of ln(x) The derivative of ln(x) is 1/x and is actually a wellknown derivative that most put to memory However, it's always useful to know where this formula comes from, so let's take a look at the steps to actually find this derivativeLogarithmic differentiation Calculator online with solution and steps Detailed step by step solutions to your Logarithmic differentiation problems online with our math solver and calculator Solved exercises of Logarithmic differentiationI want to take derivative of g with respect to ln x, ie dg/d ln x where g= ax^2/(1ax^2/r^2) Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers




Math 6c Chapter 12 Quiz Solutions




Partial Differentiation And Multiple Integrals Pdf Free Download
Find the derivative of y with respect to x y = ln x^3 dy/dx = A) 1/x^3 B) 3/x^2 C) 3/x D) 3x E) none of these Suppose that F(x) = f(g(x)) and g(14) = 2, g'(14) = 5, f'(14) = 15, Find F'(14) A) 60 B) 140 C) 24 D) 17 E) middotIf f(t) = Squareroot 4t 1, find f'(2) f'(2) = A) 4/27 B)Derivative of y ln u where u is a function of x Free derivative calculator differentiate functions with all the steps Advanced math solutions derivative calculator implicit differentiation Find the derivative of y ln 1 x 2 1 2 if you could show work i would appreciate as iA constant and the derivative of x2 with respect to x is 2x For the second part x2 is treated as a constant and the derivative of y3 with respect to is 3 2 Exercise 1 Find ∂z ∂x and ∂z ∂y for each of the following functions (Click on the green letters for solutions) (a) z = x2y4, (b) z = (x4 x2)y3, (c) z = y12 sin(x)




Calculus Derivative Of The Natural Log Ln Video Lessons Examples Solutions




X Ln Y Y Ln X 2 Ln Y X Ln X Y 2 Ln X 2 Chegg Com
Free derivative calculator differentiate functions with all the steps Type in any function derivative to get the solution, steps and graphHolds, then y is implicitly defined as a function of x The partial derivatives of y with respect to x 1 and x 2, are given by the ratio of the partial derivatives of F, or ∂y ∂x i = − F x i F y i =1,2 To apply the implicit function theorem to find the partial derivative of y with respect to x 1 (for example), first take the total1 Find the derivative, with respect to x, of each of the following functions (in each case y depends on x) a) y b) y2 c) siny d) e2y e) xy f) xy g) ysinx h) ysiny i) cos(y2 1) j) cos(y2 x) 2 Differentiate each of the following with respect to x and find dy dx a) siny x2 4y = cosx b) 3xy2 cosy2 = 2x3 5 c) 5x2 − x3 siny 5xy = 10




Find The Partial Derivative Of F X Y E X2 Y2 With Chegg Com




Show That Z Ln X 2 Y 2 2 Tan 1 Y X Satisfies The Laplaces S Equation Mathematics Stack Exchange
Online Question and Answer in Differential Calculus (Limits and Derivatives) Series Following is the list of multiple choice questions in this brand new series MCQ in Differential Calculus (Limits and Derivatives) PART 1 MCQ from Number 1 – 50 Answer key PART 1 PART 2 MCQ from Number 51 – 100 Answer key PART 2Once again I have some crazy relationship between x and y and just to get a sense of what this might look like if you plot all the X's and Y's that satisfy this relationship you get this nice little clover pattern and I plotted this off of Wolfram Alpha but what I'm curious about in this video is you might imagine from the title is to figure out the rate at which Y is changing with respect toWe know that, if mathy=ln(x)/math math\dfrac{dy}{dx}=\dfrac{1}{x}/math when we have simply mathx/math if mathu=x/math, math\dfrac{du}{dx}=\dfrac
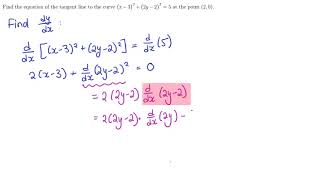



Implicit And Logarithmic Differentiation




Derivative Of Ln X Natural Logarithm More
Answer to Use logarithmic differentiation to find the derivative of y with respect to the given independent variable y = (sin 8 x)^{2 x} By Just to show the versatility of calculus, we can solve this problem through implicit differentiation Raise both side to the power of e y = ln(x2) ey = eln(x2) ey = x2 Differentiate both sides with respect to x The left side will require the chain rule ey( dy dx) = 2x dy dx = 2x eyTherefore, diff computes the second derivative of x*y with respect to x syms x y Df = diff(x*y,2) Df = 0 sym(0) If you use nested diff calls and do not specify the differentiation variable, diff determines the differentiation variable for each call




Implicit Derivation Of Logarithmic Function Y Ln X 2 Y 2 Youtube
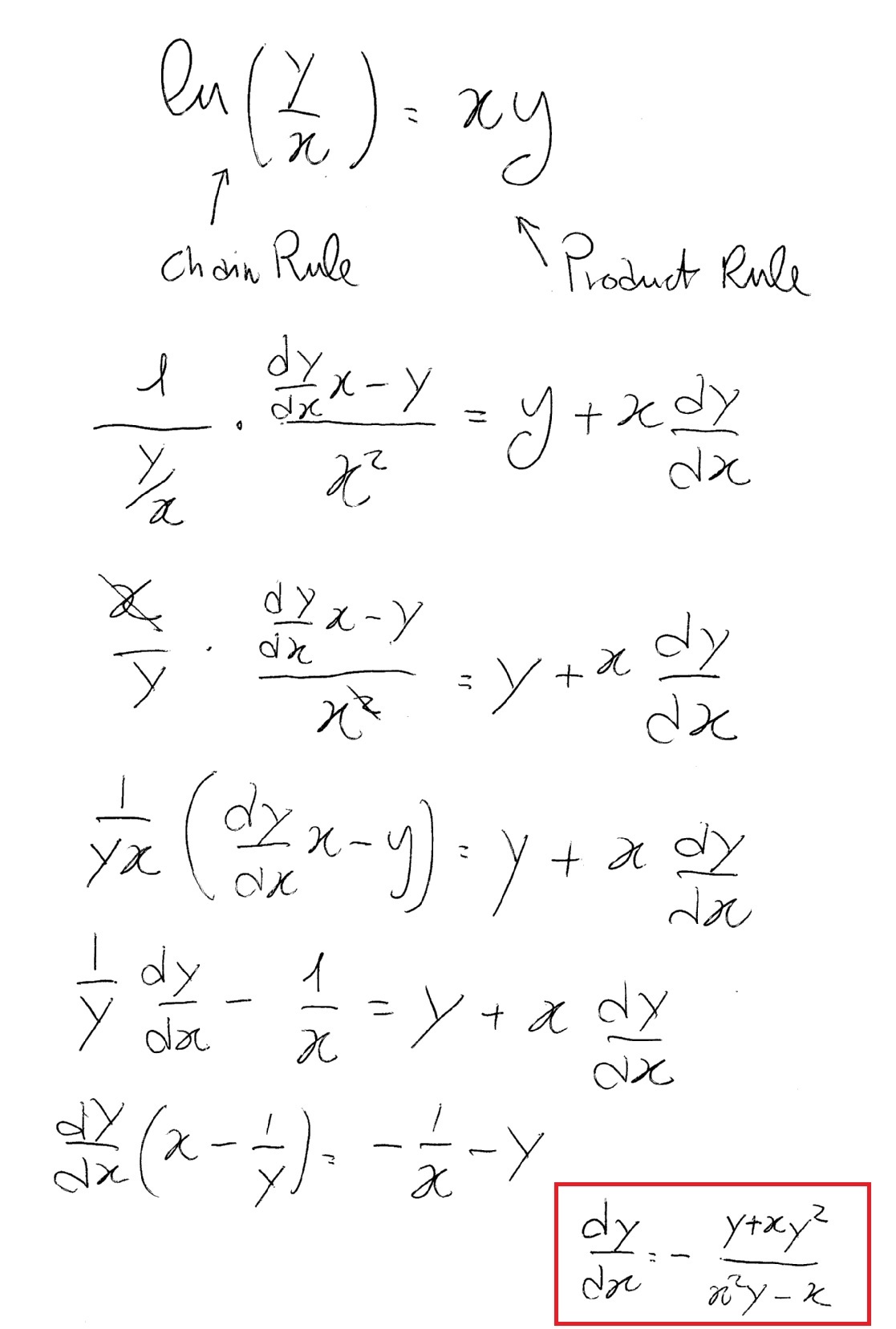



How Do You Differentiate Ln Y X Xy Socratic
In doing this, the Derivative Calculator has to respect the order of operations A specialty in mathematical expressions is that the multiplication sign can be left out sometimes, for example we write "5x" instead of "5*x" The Derivative Calculator has to detect these cases and insert the multiplication signJenna Long, 25 Honda Agent Thanks On minus the lock base five After squaring of the X and the question asked to find a white Bram recorder, it will have the block based I off the function of the X the river to which you get me coach you Did you prime the X divided by you of the X Times onlineDerivative of arctanx at x=0;




Differentiate The Function W R T X X X 2 Sinx



5 Derivative Of The Logarithmic Function
Derivative of ln(x^2) Applying the chain rule, along with the derivatives d/ d x ln (x) = 1/ x and d/ d x(x²) = 2 x, we have derivative of ln(x^2) Derivative of ln(3x) to find out the derivative of ln (3 x) then suppose that ln (3 x) = y e^ y = 3 x Now use implicit differentiation Remember that d y/ d y ⋅ d y/ d x = d y/ d x If youDifferentiate (x^2 y)/ Given a function , there are many ways to denote the derivative of with respect to The most common ways are and When a derivative is taken times, the notation or is used These are called higherorder derivatives//googl/JQ8NysPartial Derivative of f(x, y) = xy/(x^2 y^2) with Quotient Rule
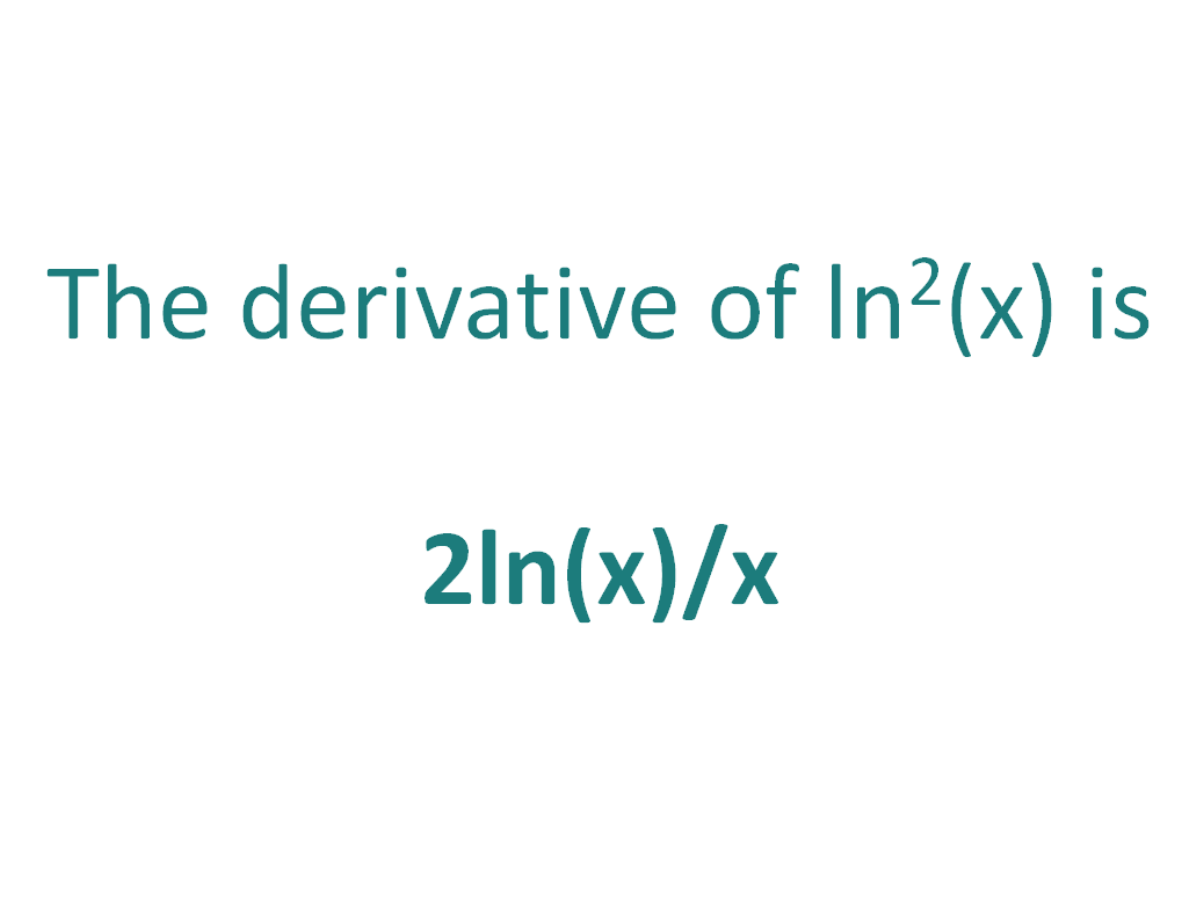



The Derivative Of Ln 2 X Derivativeit




Second Derivative Of Ln X Sqrt 1 X 2 Youtube
Find the Derivative f(y)=y/(x^2y^2) Differentiate using the Quotient Rule which states that is where and Multiply by By the Sum Rule, the derivative of with respect to is Since is constant with respect to , the derivative of with respect to is Add and Differentiate using the Power Rule which states that is where Multiply byAnswer to Find the partial derivative of the function z=ln (xy) By signing up, you'll get thousands of stepbystep solutions to your homeworkDerivative x^2(xy)^2 = x^2y^2 Natural Language;




Derivative Calculator Wolfram Alpha



How Do You Determine Whether The Function F X Ln X 2 7 Is Concave Up Or Concave Down And Its Intervals Socratic
Derivative of y = ln u (where u is a function of x) Unfortunately, we can only use the logarithm laws to help us in a limited number of logarithm differentiation question types Most often, we need to find the derivative of a logarithm of some function of xFor example, we may need to find the derivative of y = 2 ln (3x 2 − 1) We need the following formula to solve such problemsBy Staff Writer Last Updated Follow Us The derivative of y = xln (x) with respect to x is dy/dx = ln (x) 1 This result can be obtained by using the product rule and the wellknown results d (ln (x))/dx = 1/x and dx/dx = 1 The product rule of differentiation states that the derivative of aI need to take the derivative of a long function with respect, the function is already in logs Something like log(y) = 10 clog(d)log(x) axb I am guessing the last part should be come abx But I am using methods that I haven't used before daxb d lnx = a xb d lnx = a ( dxbxb − 1) dx / x simplifying to abx Thanks in advance




Section 3 5 Find The Derivative Of G X X 2 Ln X Ppt Video Online Download




What Is The Differentiation Of X 2 Quora
The required derivative of `y = x^(ln x)` is `dy/dx = 2*ln x*x^(ln x 1)` Approved by eNotes Editorial Team Ask a Question Ask a Question Submit Question Popular Questions See allExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyI'll assume that you want to compute the derivative of mathy/x/math with respect to mathx,/math and that mathy/math is a function of mathx/math Use the quotient rule which in general says that math\displaystyle\left(\frac
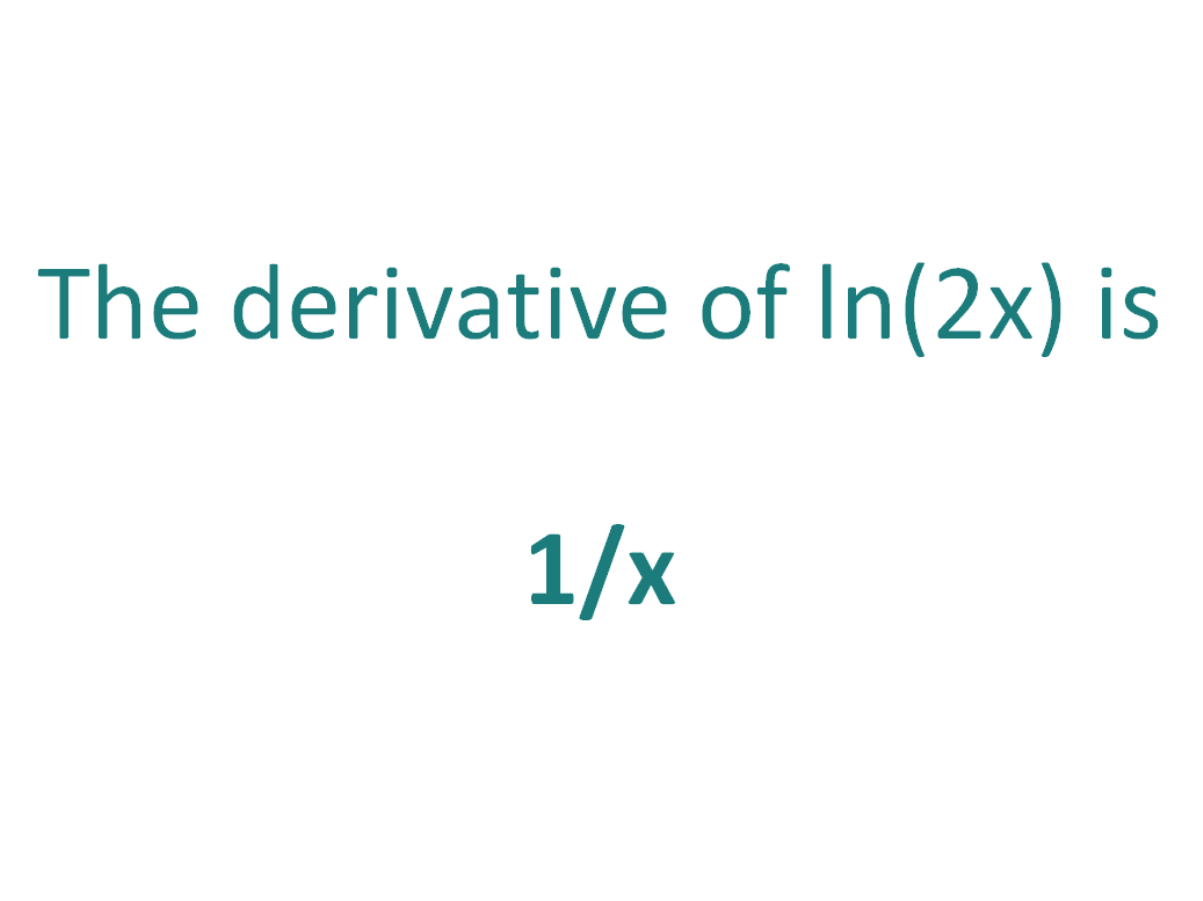



The Derivative Of Ln 2x Derivativeit



Solved Take The Derivative And Isolate Dy Dx In The Equation X Y Lnx 2 Sin Y Course Hero
Calculus Find the Derivative f (y) = square root of x^2y^2 f (y) = √x2 y2 f ( y) = x 2 y 2 Use n√ax = ax n a x n = a x n to rewrite √x2 y2 x 2 y 2 as (x2 y2)1 2 ( x 2 y 2) 1 2 d dx (x2 y2)1 2 d d x ( x 2 y 2) 1 2 Differentiate using the chain rule, which states that d dx f (g(x)) d d x f ( g ( x)) is f '(g(x))g



How Do You Find The Derivative Of Y Ln X Sqrt 1 X 2 1 Sqrt2 Socratic




3 9 Derivatives Of Ln General Exponential Log Functions And Logarithmic Differentiation Mathematics Libretexts
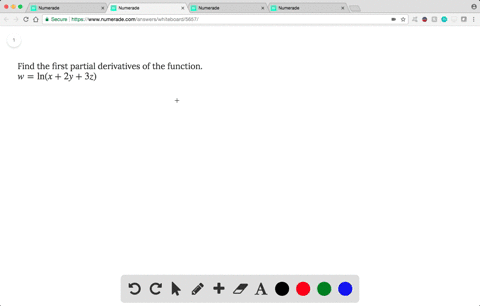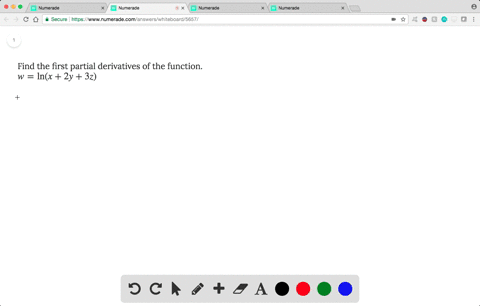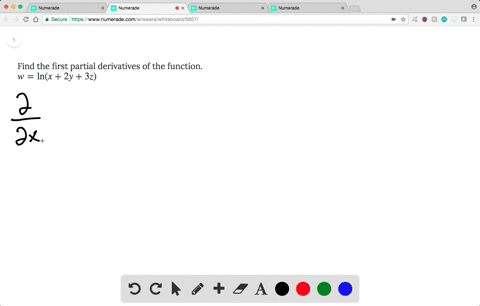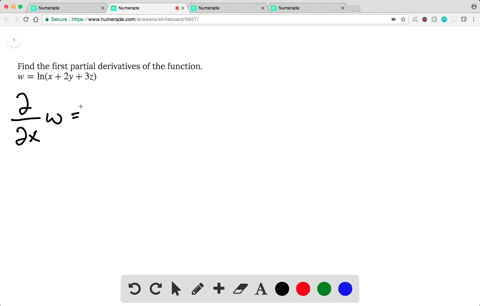



Solved Find The First Partial Derivatives Of The Function W Ln X 2y 3z
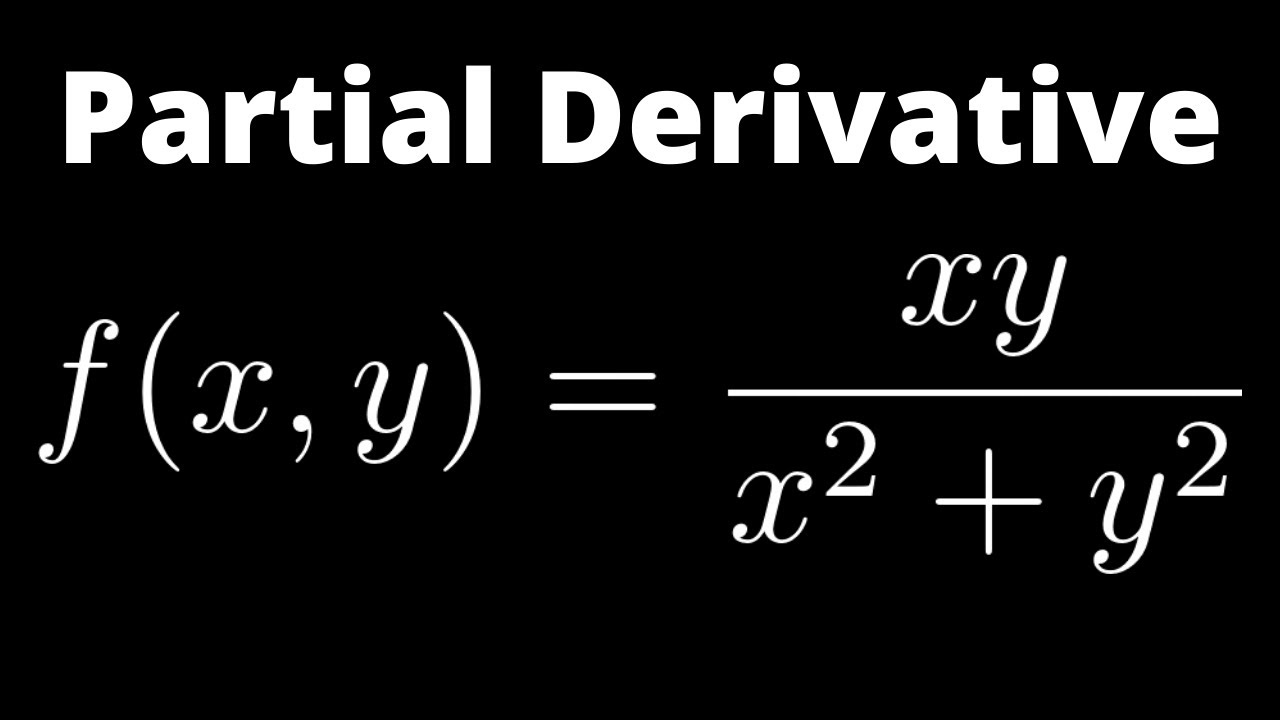



Partial Derivative Of F X Y Xy X 2 Y 2 With Quotient Rule Youtube
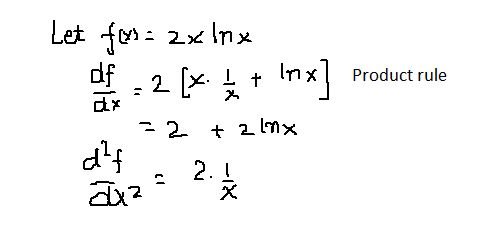



How Do You Find The First And Second Derivative Of 2x Ln X Socratic
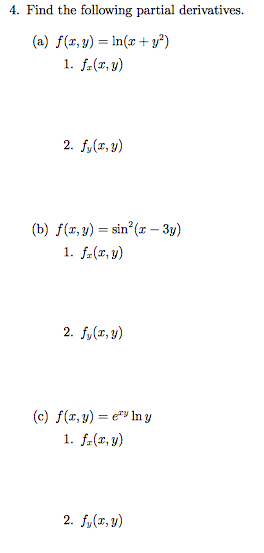



4 Find The Following Partial Derivatives A Chegg Com



Rpubs Com Venkatritch
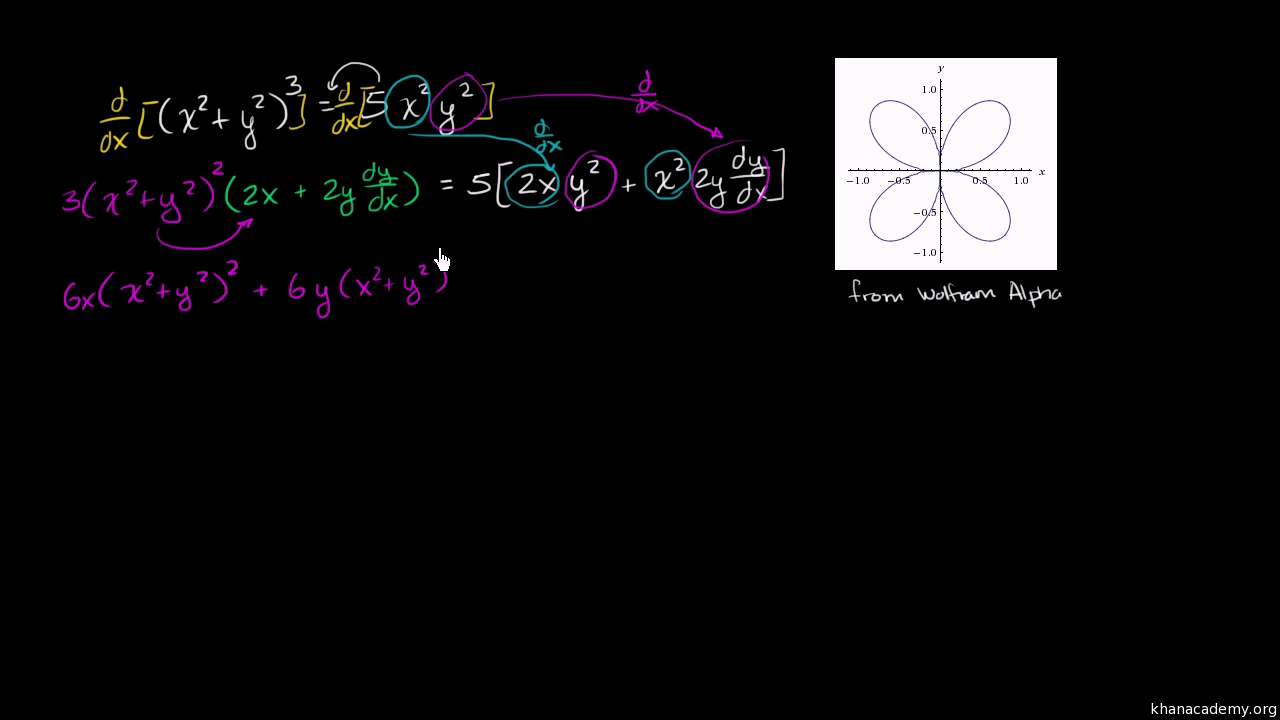



Implicit Differentiation Advanced Example Video Khan Academy



What Is The Differentiation Of Ln Sinx Quora



Http Www Stat Wisc Edu Ifischer Calculus Pdf
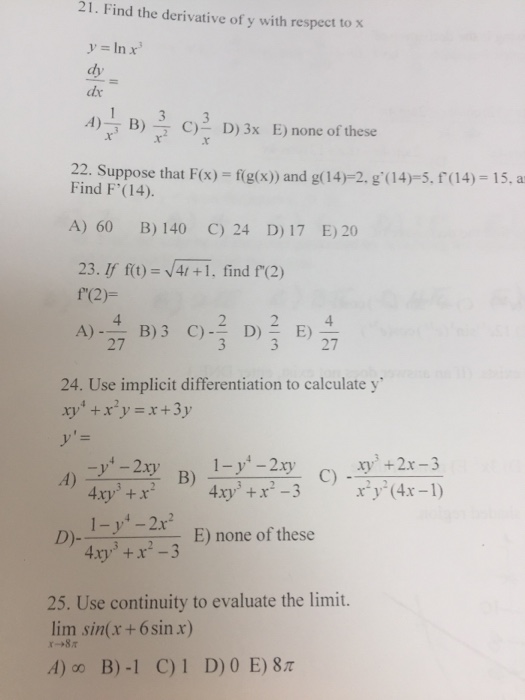



Find The Derivative Of Y With Respect To X Y Ln Chegg Com




Derivative Of Ln X Natural Logarithm More




First Order Partial Derivatives Of F X Y Ln X 4 Y 4 Youtube




Differential Calculus Concepts Problems 126 Rd 1 Matrix
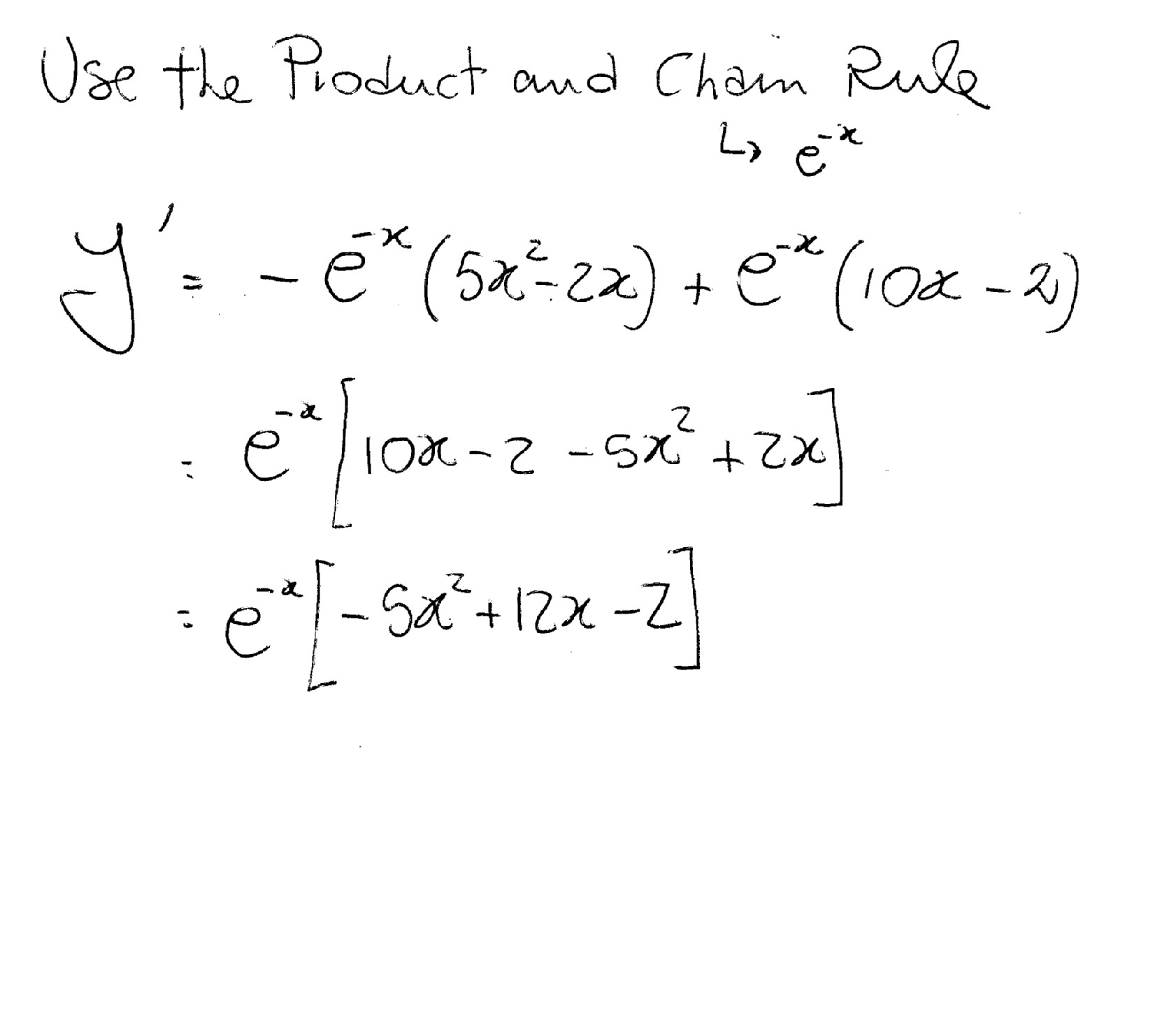



How Do You Find The Derivative Of Y E X 5x 2 2x Socratic




Derivative Wikipedia




How To Do Implicit Differentiation 7 Steps With Pictures



What Is The Differentiation Of The Log Of X Square Plus Y Square Quora




Derivative Rules




How To Differentiate 2 2x Quora
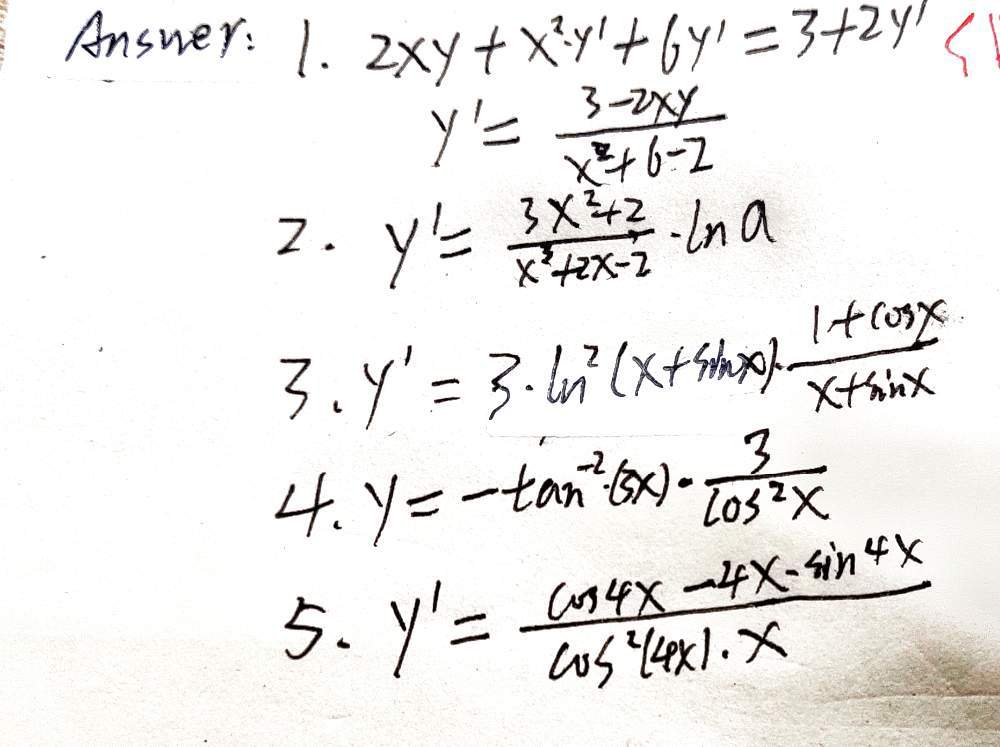



Learning Task 1 Determine The Derivative Of The F Gauthmath




Help Please For 1 2 6 Find The First Order Partial Chegg Com




The Natural Logarithmic Function Ppt Download



Www Princeton Edu Dixitak Teaching Microhighcalculus Precepts Prcpt03 Pdf




Proof The Derivative Of Ln X Is 1 X Video Khan Academy




Derivative Wikipedia




Find The First Derivative Of The Function Y Ln X Gauthmath




8 Find All Second Order Partial Derivatives For The Chegg Com



If U Log X 2 Y 2 Xy Then X U X Y U Y Is A 0 B U C 2u Sarthaks Econnect Largest Online Education Community




4 2 Derivatives Of Logarithmic Functions



Derivative Calculator With Steps



Www3 Nd Edu Taylor Math550 Images Oldexams Exam2a Pdf




Derivative Of Ln X Video Khan Academy




Integration By Parts Wikipedia




Lesson 13 Derivatives Of Logarithmic And Exponential Functions




Find Derivative Of Y E Sqrt Sin Ln X 2 7 5




How To Do Implicit Differentiation 7 Steps With Pictures



Http Math Utoledo Edu Dwhite1 D 1850 Q6a1850s Pdf
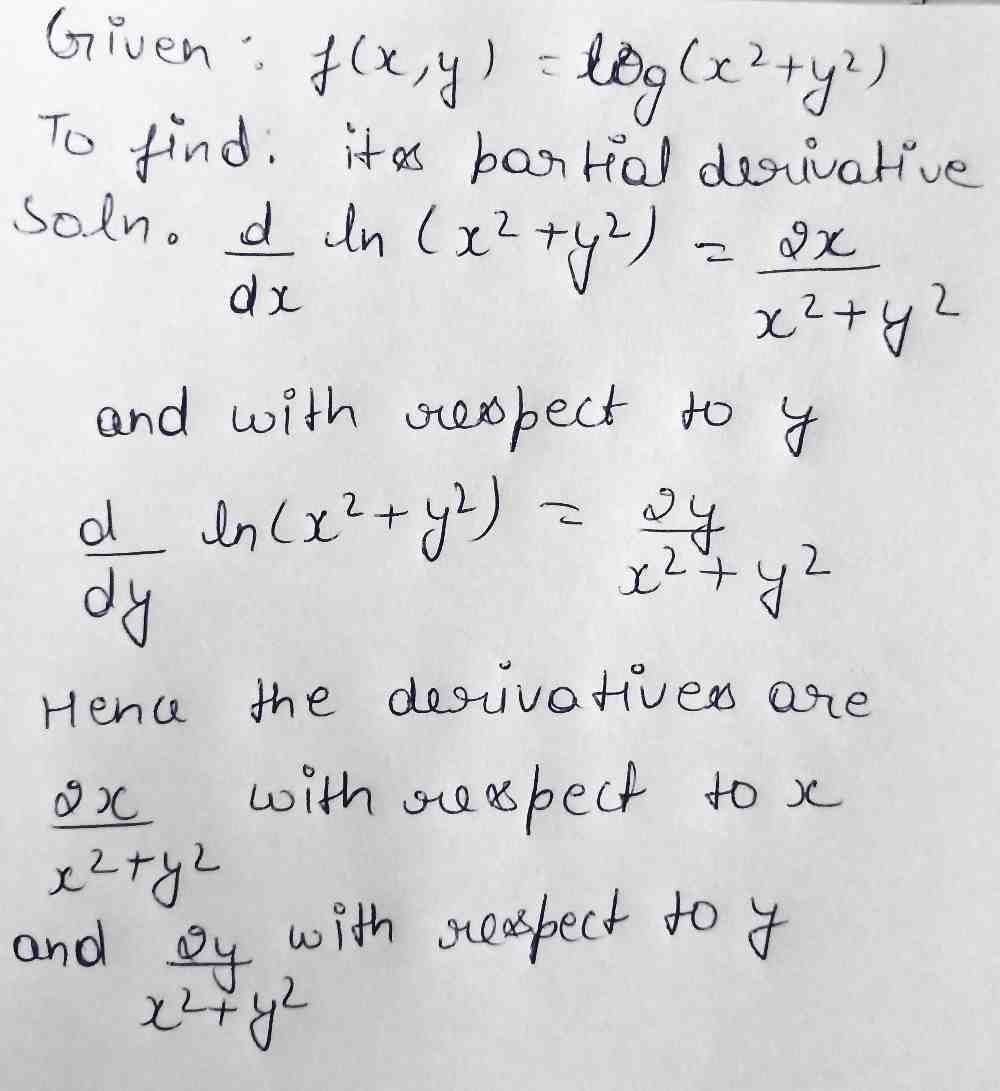



Partial Derivative Of Fx Y Ln X2 Y2 Gauthmath



Www Math Colostate Edu Clayton Teaching M113f09 Homework Hw7solutions Pdf



Www Berkeleycitycollege Edu Kpernell Files 13 02 12fall Ch3 Derivatives Practice Probs Key Pdf




Question Video Differentiating Logarithmic Functions Using The Chain Rule Nagwa




Find The First Derivative And Second Derivative Of Given Functions Wr T The Independent Variable X Y Ln X 2 Sin X




If X T 2 Y T 3 Then D 2y Dx 2 3 2 B 3 4t C 3 2t D 3t 2



Jntua Ac In Gate Online Classes Registration Downloads Material A Pdf




The Derivative Of E X And Lnx
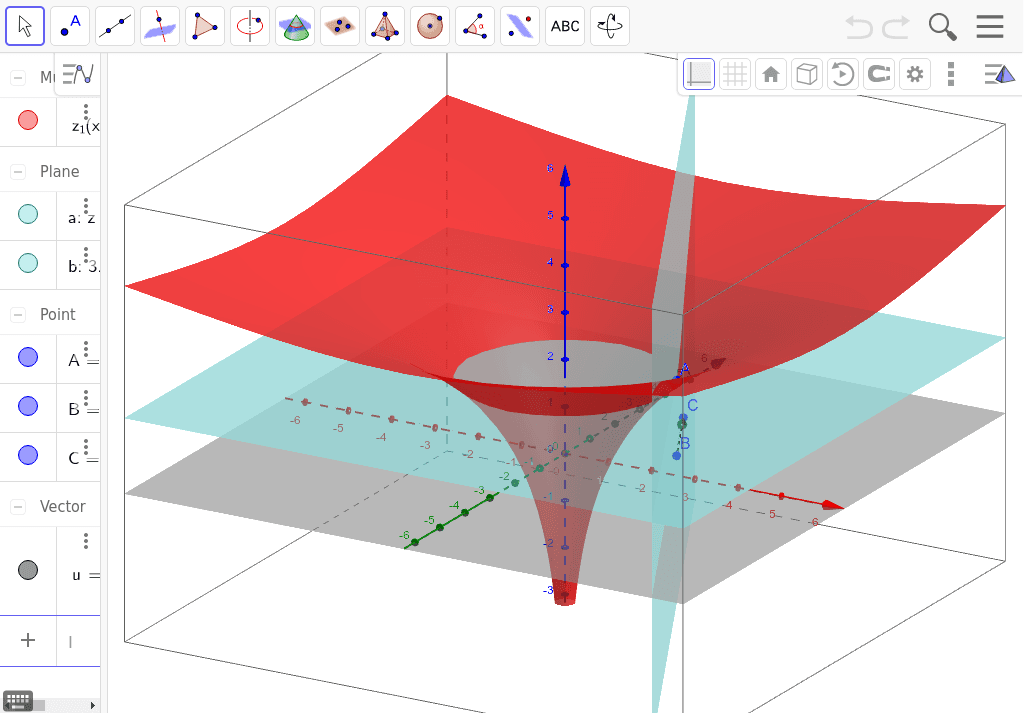



Ln X 2 Y 2 With Directional Derivative Geogebra




Find Y For Ln X Y Arctan Xy Mathematics Stack Exchange




Calculating The Derivative Of Ln X 2 Video Lesson Transcript Study Com



Ovingtonclassroom Weebly Com Uploads 1 0 6 2 Chapter 4 Review Key Pdf




Differential Equations Separation Of Variables Ppt Download
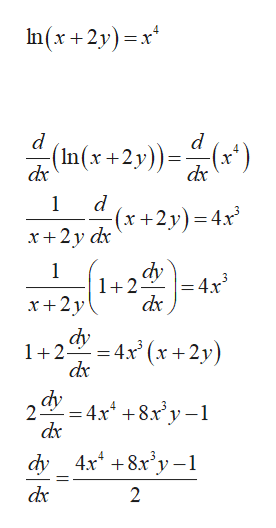



Answered Suppose Ln X 2y X4 Use Implicit Bartleby



3




Calculating The Derivative Of Ln X 2 Video Lesson Transcript Study Com



Www Whitman Edu Mathematics Multivariable Multivariable 14 Partial Differentiation Pdf




5 5 The Differentiation Of Logarithmic Functions Let Y Ln X X 0
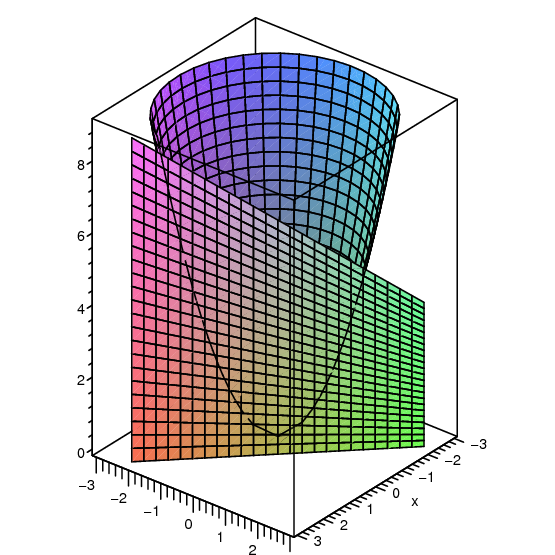



14 3 Partial Differentiation




Implicit Differentiation



1
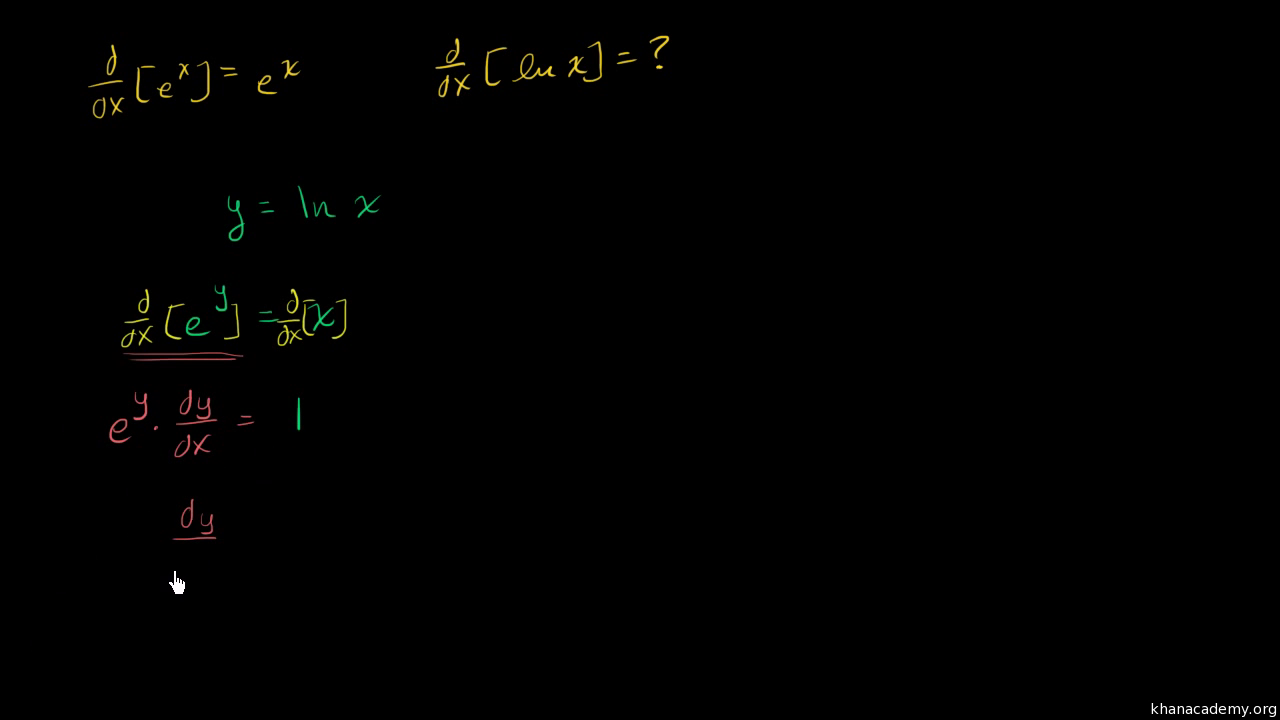



Derivative Of Ln X From Derivative Of 𝑒ˣ And Implicit Differentiation Video Khan Academy




The Derivative Of Lnx And Examples Mathbootcamps




24 Questions With Answers In Natural Logarithm Science Topic




5 Derivative Of The Logarithmic Function




Find The Derivative Of The Function Y Ln 4 Chegg Com



Jntua Ac In Gate Online Classes Registration Downloads Material A Pdf




Ppt Section 3 5 Find The Derivative Of G X X 2 Ln X You Will Need To Use The Product Rule Powerpoint Presentation Id




Ex 6 2 7 Show That Y Log 1 X 2x 2 X Is An Increasing Fn
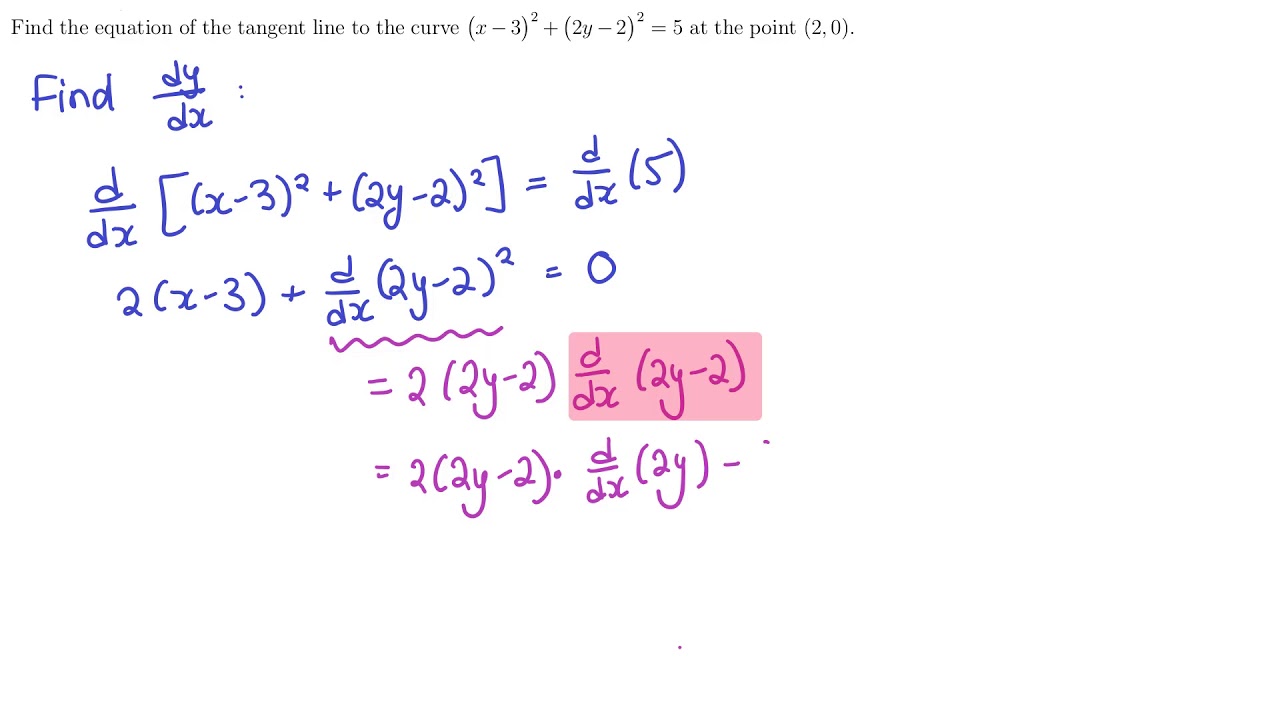



Implicit And Logarithmic Differentiation



3 8 Implicit Differentiation Calculus Volume 1




Solving The Derivative Of Ln X Video Lesson Transcript Study Com




Ex 3 Find A Value Of A Directional Derivative F X Y Ln X 2 Y 2 Youtube
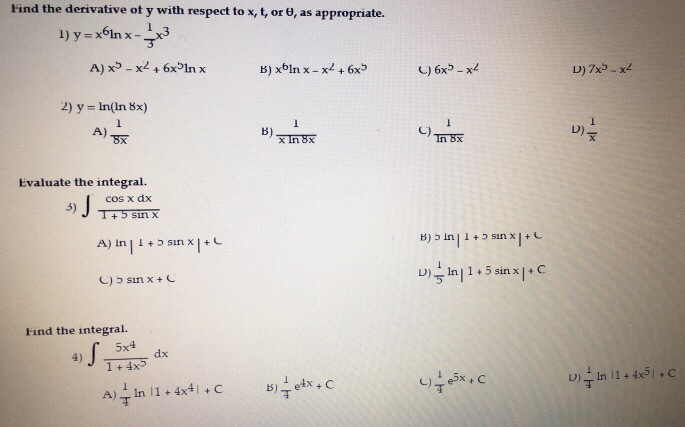



Find The Derivative Of Y With Respect To X T Or Theta Chegg Com



1



3 8 Implicit Differentiation Calculus Volume 1




Solving The Derivative Of Ln X Video Lesson Transcript Study Com




Implicit And Logarithmic Differentiation



No comments:
Post a Comment